Bisection Method - Half-interval Search

This code calculates roots of continuous functions within a given interval and uses the Bisection method. The program assumes that the provided points produce a change of sign on the function under study. If a change of sign is found, then the root is calculated using the Bisection algorithm (also known as the Half-interval Search). If there is no change of sign, an error is displayed. You could try with other low or high values, or you could improve the code to find two values with a different sign before going on.

In general, when we work with numerical methods we must be aware that errors may result for a number of reasons. First, a root may be calculated when it should not be. It could happen if a point is so close to zero that a root is found due to round-off error. Second, two roots may be so close together that the program never finds the opposite signs between them... 

You will provide the function, the interval (both low and high values) and a tolerance. This suggested version of the method will list the evaluated intervals and the final approximation found using your tolerance.

function  m = bisection(f, low, high, tol)
disp('Bisection Method'); 

% Evaluate both ends of the interval
y1 = feval(f, low);
y2 = feval(f, high);
i = 0; 

% Display error and finish if signs are not different
if y1 * y2 > 0
   disp('Have not found a change in sign. Will not continue...');
   m = 'Error'
   return
end 

% Work with the limits modifying them until you find
% a function close enough to zero.
disp('Iter    low        high          x0');
while (abs(high - low) >= tol)
    i = i + 1;
    % Find a new value to be tested as a root
    m = (high + low)/2;
    y3 = feval(f, m);
    if y3 == 0
        fprintf('Root at x = %f \n\n', m);
        return
    end
    fprintf('%2i \t %f \t %f \t %f \n', i-1, low, high, m);   

    % Update the limits
    if y1 * y3 > 0
        low = m;
        y1 = y3;
    else
        high = m;
    end
end 

% Show the last approximation considering the tolerance
w = feval(f, m);
fprintf('\n x = %f produces f(x) = %f \n %i iterations\n', m, y3, i-1);
fprintf(' Approximation with tolerance = %f \n', tol); 

and want to explore the interval [0.1, 0.5], we could call the function from another m-file, like this: 

my_fun = @(x) 5*x^4 - 2.7*x^2 - 2*x + .5;
low = .1;
high = 0.5;
tolerance = .00001;
x = bisection(my_fun, low, high, tolerance); 

the result is:
 

Bisection Method
Iter    low        high          x0
 0     0.100000    0.500000    0.300000
Root at x = 0.200000
 

If we plot the function, we get a visual way of finding roots. In this case, this is the function 

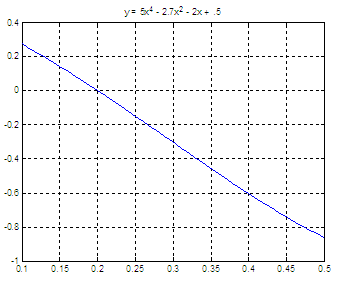
Now, another example and let’s say that we want to find the root of another function 
y = 2.5x² - 3x + 0.5 

using another interval, like [0, 0.5], we can use this code to call the half-interval search 

my_fun = @(x) 2.5*x^2 - 3*x + .5;
low = 0;
high = 0.5;
tolerance = .00001;
x = bisection(my_fun, low, high, tolerance);

and we get this information from the proposed code above:
 

Bisection Method
Iter    low        high          x0
 0     0.000000    0.500000    0.250000
 1     0.000000    0.250000    0.125000
 2     0.125000    0.250000    0.187500
 3     0.187500    0.250000    0.218750
 4     0.187500    0.218750    0.203125
 5     0.187500    0.203125    0.195313
 6     0.195313    0.203125    0.199219
 7     0.199219    0.203125    0.201172
 8     0.199219    0.201172    0.200195
 9     0.199219    0.200195    0.199707
10     0.199707    0.200195    0.199951
11     0.199951    0.200195    0.200073
12     0.199951    0.200073    0.200012
13     0.199951    0.200012    0.199982
14     0.199982    0.200012    0.199997
15     0.199997    0.200012    0.200005 

 x = 0.200005 produces f(x) = -0.000009
 15 iterations
 Approximation with tolerance = 0.000010 

Again, plotting the function is a good idea to better know what we’re doing...
 

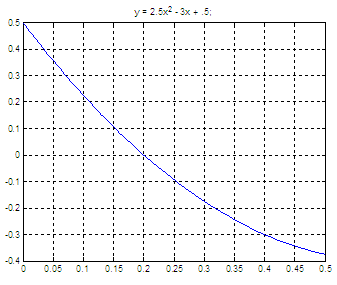
Maybe you're also interested in:

Finding intersections

Other ideas about root finding

Nonlinear systems