Exponential decay – Half life formulaDecay calculator in Matlab
The formulas below are used in calculations involving the exponential decay of, for example, radioactive materials 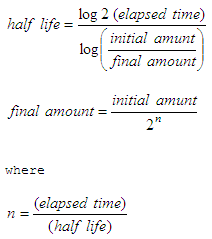 Let’s code a Matlab
function to calculate the final amount
of a substance, given the elapsed time, half-life and initial amount.
This is
just a code of the ‘final amount’ formula above function end_amt
= exp_decay(beg_amt, hl, time) This is a possible code
to calculate the half-life of a
substance, if we’re given the initial and final amounts, and the
elapsed time
between those masses: function hl =
half_life(beg_amt, fin_amt, time) And this code calculates the time needed for a substance undergoing exponential decay to go from an initial mass to a final mass. We need to know the half-life, naturally. function t =
elapsed_time(beg_amt, fin_amt, hl) Now, let’s test our decay
calculators to discover ending
amounts: if we start with 100 grams of radium, and we know its
half-life is
1620 years, how much would be left after 3240 years (two half-lives)? We can type this from the
command window or from any other
script. It’s important to follow the order of the parameters: end_amt
= exp_decay(100, 1620, 3240)
end_amt
= exp_decay(10, 1690, 50) The result on screen is end_amt = 9.7970
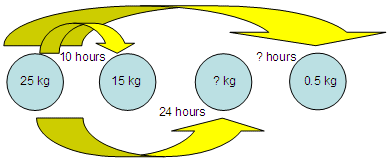
Let’s suppose that salt decomposes in water into chloride and sodium ions according to the law of exponential decay. If the initial amount of salt is 25 kg and after 10 hours, 15 kg of salt is left, how much salt is left after 1 day? How long does it take until 0.5 kg of salt is left? We need to understand
what we’re being asked. We can make a
drawing to understand better...
We could create an m-file named ‘test_exp_decay’, for example, and we’d type this: clear,
clc, format compact %
Initial amount of salt is 25 kg %
How much salt is left after 1 day? The code represents the given problem and its solution. First, we solve for the half-life; second, we solve for the ending amount; finally, we solve for the elapsed time considered in the formulas. Matlab answer is: hl = 13.5692 From 'Exponential Decay' to home From 'Exponential Decay' to Matlab Tutorials
|