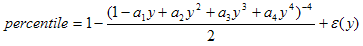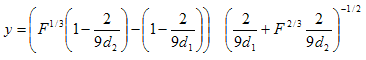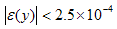F-distribution
This algorithm (program in Matlab) calculates percentile values for
given values on an F-distribution curve.
|
You must provide the value
of F,
the degrees of freedom
in the numerator and the degrees of freedom in the
denominator. This Matlab code does not use any special
toolbox, it uses only standard built-in functions.
|
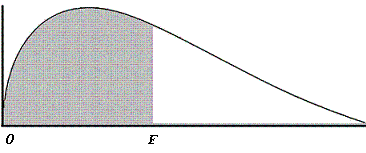 |
| The
F-distribution
curve |
The area of the shaded region represents the percentile. The tail-end
value (the area of the unshaded region) is also calculated.
The F-distribution
function is approximated using the following formula:
where,
a1
=
0.196854
a2
=
0.115194
a3
=
0.000344
a4
=
0.019527
d1 =
degrees of freedom in numerator
d2
=
degrees of freedom in denominator
This is the Matlab script to perform the task:
clc;
clear
%
Asks the
user for the relevant input
f
= input ('Enter
F-value: ');
d1 = input('Enter
degrees
of freedom in numerator: ');
d2 = input('Enter
degrees
of freedom in denominator: ');
x
= 1;
%
Computes
using inverse for small F-values
if
f < 1
s
= d2;
t
= d1;
z
= 1/f;
else
s = d1;
t
= d2;
z
= f;
end
j
= 2/(9*s);
k = 2/(9*t);
%
Uses
approximation formulas
y
= abs((1 -
k)*z^(1/3) - 1 + j)/sqrt(k*z^(2/3) + j);
if
t < 4
y
= y*(1 + 0.08*y^4/t^3);
end
a1
= 0.196854;
a2 = 0.115194;
a3 = 0.000344;
a4 = 0.019527;
x = 0.5/(1 +
y*(a1 + y*(a2 + y*(a3 + y*a4))))^4;
x =
floor(x*10000 + 0.5)/10000;
%
Adjusts
if inverse was computed
if
f < 1
x
= 1 - x;
end
%
Displays
results
str1
= ['Percentile
=
'
num2str(1-x)];
str2 = ['Tail
end
value = '
num2str(x)];
disp(str1)
disp(str2)
Example 1 - Calculate a percentile
What is
the percentile on an F-distribution curve when the F-value is 0.474 and
the degrees of freedom are 1 and 18?
We run
the code above and enter the data:
Enter F-value: .474
Enter degrees of freedom in numerator: 1
Enter degrees of freedom in denominator: 18
Matlab response is:
Percentile
= 0.4937
Tail end
value = 0.5063
Example
2
What is
the percentile the F-value is 23.7 and the degrees of freedom
are 3 and 6?
We run
the code above and enter the data:
Enter F-value: 23.7
Enter degrees of freedom in numerator: 3
Enter degrees of freedom in denominator: 6
Matlab response is:
Percentile
= 0.9984
Tail end
value = 0.0016
From
'F-distribution' to
Matlab home
From
'F-distribution' to 'Probability and Stats'


|