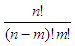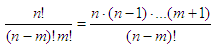Factorials
– several ideas to code them
Four methods to code and calculate factorials
In
mathematics, factorials
of positive integers n, are the
product of all positive
integers less than or equal to n.
Factorials are denoted by n!.
For example:
6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Note: 0! is a special case that is defined as 1.
The factorial operation
is found in many areas of math, mainly
in probability and statistics, combinatorics, algebra and data
analysis. Its
most basic appearance is due to the fact that there are n!
ways to arrange n
distinct elements into a sequence (permutations of any set of objects).
There are a number of
solutions when we have to code
factorials and we can experiment with any number-crunching software.
1. Function ‘factorial’
In
Matlab, we can use built-in function ‘factorial’, like
this:
n = 9
%
use function factorial
factorial(n)
The answer is 362880.
2. Function ‘prod’
We can also use built-in
function ‘prod’. For vectors,
prod(n) is the product of the elements of n. For matrices, prod(X) is a
row
vector with the product of each column.
n = 9
%
use function prod, which multiplicates
%
every element in a vector
prod([1
: n])
The answer is, again,
362880.
3. Iterations
We can
use iterations to get the multiplication of numbers,
just following the definition of what a factorial is
n = 9
%
use iterations
f
= 1;
for i = 1:n
f
= f*i;
end
f
4.
Recursion
We could even use a
recursive method to calculate a
factorial. That idea and method is explained in
detail in the
article recursion.
Custom-made formula
Now, if we want to
calculate a custom-made formula including
factorial operations, we can create and optimize a function for that
specific purpose.
Let’s say that we need to calculate
without
using the Matlab factorial function. As a condition,
we may assume that the user will know that n
> m, and that n
and m are positive
integers.
We can optimize the code,
since we know in advance that
Thus, our customized
function could be:
function y =
special_fact(n, m)
%
using 'prod' and appropriate vectors
y =
prod([m+1 : n]) / prod([1 : n-m]);
or another possibility
function y =
special_fact1(n, m)
%
using loops to calculate the numerator
f1
= 1;
for i = m+1
: n
f1
= f1 * i;
end
%
using loops to calculate the denominator
f2
= 1;
for i = 1 :
n-m
f2
= f2 * i;
end
%
assembling the appropriate terms
y
=
f1/f2;
Let’s test our functions:
n = 19;
m = 13;
factorial(n)/(factorial(n-m)*factorial(m))
special_fact(n,m)
special_fact1(n,m)
And all the answers are
27132.
Double Factorials
A note on double factorials... Mathematically, the formulas for DF are
as follow.
If n is even, then
n!! = n(n - 2)(n - 4)(n - 6)... (4)(2)
If n is odd, then
n!! = n(n - 2)(n - 4)(n - 6) ...(3)(1)
We can code that with a simple script:
n =
input('Give
me a number: ');
df = 1;
for i = n :
-2 : 1
df
= df * i;
end
str = ['Double
Factorial of '
num2str(n) '
is '
num2str(df)];
disp(str)
From
'Factorials' to Matlab
Examples home
From
'Factorials' to Calculus Problems


|