Gray Code in Matlab – from/to binary and decimal

Convert a binary number to a Gray number

 
Let’s understand the algorithm to go from binary to Gray. See the conversion from ‘11101’ binary to its equivalent in Gray code.

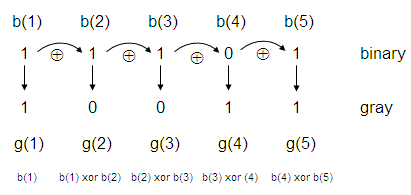
The most significant bit (MSB) in Gray is taken directly from the MSB in binary. The rest of the Gray bits comes from a xor operation between the precedent binary bit(b(i-1)) and the current binary bit (b(i)). In the case shown in the figure above:
 

g(1) = b(1)
g(2) = b(1) xor b(2)
g(3) = b(2) xor b(3)
g(4) = b(3) xor b(4)
g(5) = b(4) xor b(5)

The xor operation produces a 1 if the bits are different, and produces a 0 if the bits are equal. So, a binary ‘11101’ becomes a ‘10011’ in Gray.

Let’s propose a code in Matlab to do it. 

function g = bin2gray(b)
g(1) = b(1);
for i = 2 : length(b);
    x = xor(str2num(b(i-1)), str2num(b(i)));
    g(i) = num2str(x);
end

The input parameter to this function is a binary number (expressed in a string), the output is the equivalent Gray number (also expressed as a string).

g = bin2gray('11101')
g = bin2gray('10010')
g = bin2gray('11110')
g = bin2gray('10000')
 

We get these string-results from Matlab:

g = 10011
g = 11011
g = 10001
g = 11000

 
We also can test a full sequence. We go from decimal-to-binary (using built-in function dec2bin) and then to Gray (using our developed function), for example: 

for d = 0 : 15
    b = dec2bin(d);
    g = bin2gray(b);
    disp({d b g})
end

The results are (decimal, binary, gray): 

    [0]    '0'    '0'
    [1]    '1'    '1'
    [2]    '10'    '11'
    [3]    '11'    '10'
    [4]    '100'    '110'
    [5]    '101'    '111'
    [6]    '110'    '101'
    [7]    '111'    '100'
    [8]    '1000'    '1100'
    [9]    '1001'    '1101'
    [10]    '1010'    '1111'
    [11]    '1011'    '1110'
    [12]    '1100'    '1010'
    [13]    '1101'    '1011'
    [14]    '1110'    '1001'
    [15]    '1111'    '1000'
 

Convert a Gray number to a binary number

Now let’s understand the algorithm to go from Gray to binary. See the conversion from ‘10011’ Gray to its binary equivalent.

The most significant bit (MSB) in binary is taken directly from the MSB in Gray. The rest of the binary bits comes from a xor operation between the precedent binary bit (b(i-1)) and the current Gray bit (g(i)). In the case shown in the figure above:

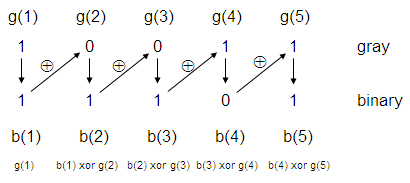
b(1) = g(1)
b(2) = b(1) xor g(2)
b(3) = b(2) xor g(3)
b(4) = b(3) xor g(4)
b(5) = b(4) xor g(5) 

Our proposed Matlab function to achieve the conversion is:

function b = gray2bin(g)
b(1) = g(1);
for i = 2 : length(g);
    x = xor(str2num(b(i-1)), str2num(g(i)));
    b(i) = num2str(x);
end

 
Let’s test our function: 

b = gray2bin('10011')
b = gray2bin('11011')
b = gray2bin('10001')
b = gray2bin('11000')
 

We get these string-results:

b = 11101
b = 10010
b = 11110
b = 10000
 

And now we test a full sequence, going decimal-to-binary, binary-to-gray, and gray-to-binary:
 

for d = 0 : 15
    g = bin2gray(dec2bin(d));
    b = gray2bin(g);
    disp({d g b})
end

We get (decimal, gray, binary):

    [0]    '0'    '0'
    [1]    '1'    '1'
    [2]    '11'    '10'
    [3]    '10'    '11'
    [4]    '110'    '100'
    [5]    '111'    '101'
    [6]    '101'    '110'
    [7]    '100'    '111'
    [8]    '1100'    '1000'
    [9]    '1101'    '1001'
    [10]    '1111'    '1010'
    [11]    '1110'    '1011'
    [12]    '1010'    '1100'
    [13]    '1011'    '1101'
    [14]    '1001'    '1110'
    [15]    '1000'    '1111'