Hex to binary: two solutions in Matlab 

To convert a value from hex to binary, we first need to know what a hexadecimal number is. 

A major numbering system used in digital systems is the hex system, also known as base 16. In this system, the numbers are counted from 0 to F. In base 16 we need 16 different symbols, decimal numbers 10 through 15 are represented by letters A through F, respectively. The  binary system (base 2) has only two symbols, '0' and '1'.

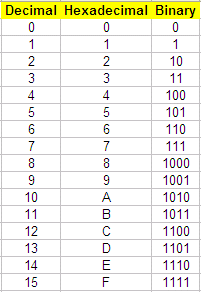
The following table shows the meaning of all the symbols in the hexadecimal  numbering system and their conversion to decimal or binary equivalents.

To convert a value from hex to binary, you merely translate each hex symbol to the equivalent 4-bit binary group. For example, the hex number A5A5 translates into the binary 1010010110100101 equivalent. 

Solution 1. 

In Matlab, we can go from decimal to binary, and then, from binary to hexadecimal. We can embed one instruction into the other, like this: 

bin_str = dec2bin(hex2dec(hex_str))

So, we can use this concept, like this:

hex_str = 'AF5'
bin_str = dec2bin(hex2dec(hex_str))

 
Matlab’s answer is: 

bin_str = 101011110101

Solution 2.

We can develop a function to translate the table shown before. Our proposed method uses a switch-case structure.

% Hex to binary conversion
function b = h2b(h)
switch h
    case {'0'}
        b = '0000';
    case {'1'}
        b = '0001';
    case {'2'}
        b = '0010';
    case {'3'}
        b = '0011';
    case {'4'}
        b = '0100';
    case {'5'}
        b = '0101';
    case {'6'}
        b = '0110';
    case {'7'}
        b = '0111';
    case {'8'}
        b = '1000';
    case {'9'}
        b = '1001';
    case {'A', 'a'}
        b = '1010';
    case {'B', 'b'}
        b = '1011';
    case {'C', 'c'}
        b = '1100';
    case {'D', 'd'}
        b = '1101';
    case {'E', 'e'}
        b = '1110';
    case {'F', 'f'}
        b = '1111';
end

Now, we have to call the function for every hex character in the string, to convert each to a 4-bit binary number. One possible solution to separate the hex characters into 4-bit groups is shown here:

hex_str = input('Enter hexadecimal number: ', 's');
n = length(hex_str); 

bin_str = '';
for h = 1 : n
    bin_str = [bin_str h2b(hex_str(h))];
end
bin_str 

Let’s try this routine. 

Enter hexadecimal number: af50
bin_str = 1010111101010000