Smith Chart – plots with Matlab

1.- Useful for visualization of radio frequency  and transmission line problems 

 
The Smith chart can be used to represent many parameters including impedances, admittances, reflection and transmission coefficients, scattering parameters... 

Normalized scaling allows the Smith chart to be used for problems involving any characteristic or system impedance which is represented by the center point of the chart. The most commonly used normalization impedance is 50 ohms. Once an answer is obtained through the graphical method, it is easy to convert between the normalized impedance and the corresponding unnormalized value by multiplying by the characteristic impedance. Reflection coefficients can be read directly from the chart. 

Use of the Smith chart and the meaning of the results obtained requires a good understanding of AC circuits and transmission line theory, both of which are needed by RF engineers. 

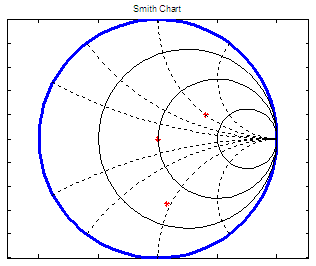
In the chart, there are horizontal circles that represent constant resistances; vertical circles represent constant reactances. The complex impedance (or admittance )is normalized using a reference, which usually is the characteristic impedance Z₀. 

The chart is part of current CAD tools and modern measurement equipments. It’s a graphic of the reflection coefficient in polar coordinates.
 

Let’s create a chart with Matlab. 

function draw_smith_chart 

% Draw outer circle
t = linspace(0, 2*pi, 100);
x = cos(t);
y = sin(t);
plot(x, y, 'linewidth', 3); axis equal; 

% Place title and remove ticks from axes
title(' Smith Chart ')
set(gca,'xticklabel',{[]});
set(gca,'yticklabel',{[]});
hold on 

% Draw circles along horizontal axis
k = [.25 .5 .75];
for i = 1 : length(k)
    x(i,:) = k(i) + (1 - k(i)) * cos(t);
    y(i,:) = (1 - k(i)) * sin(t);
    plot(x(i,:), y(i,:), 'k')
end 

% Draw partial circles along vertical axis
kt = [2.5 pi 3.79 4.22];
k = [.5 1 2 4];
for i = 1 : length(kt)
    t = linspace(kt(i), 1.5*pi, 50);
    a(i,:) = 1 + k(i) * cos(t);
    b(i,:) = k(i) + k(i) * sin(t);
    plot(a(i,:), b(i,:),'k:', a(i,:), -b(i,:),'k:' )
end

2.- Calculate the Reflection Coefficient, VSWR and Return Loss   

Now, let’s prepare some formulas to calculate typical values used in RF theory. To plot a reflection coefficient we need a normalized impedance with magnitude and angle. It’s a good idea to deliver the angle in degrees to make it easier to visualize, and also let’s calculate the Voltage Standing Wave Ratio (VSWR) and the return loss.

function [m, thd, SWR, rloss] = smith_ch_calc(Z0, Zl) 

% Draw appropriate chart
draw_smith_chart 

% Normalize given impedance
zl = Zl/Z0; 

% Calculate reflection, magnitude and angle
g = (zl - 1)/(zl + 1);
m = abs(g);
th = angle(g); 

% Plot appropriate point
polar(th, m, 'r*') 

% Change radians to degrees
thd = th * 180/pi; 

% Calculate VSWR and return loss.
% We can add epsilon to magnitude, to avoid div by 0 or log(0)
SWR = (1 + m)/(1 - m + eps);
rloss = -20 * log10(m + eps);

 
Now, let’s try our functions:

clear, clc, close all, format compact
[m1, d1, VSWR1, Rloss1] = smith_ch_calc(50, 50)
[m2, d2, VSWR2, Rloss2] = smith_ch_calc(50, 100 + 50j)
[m3, d3, VSWR3, Rloss3] = smith_ch_calc(50, 30 - j*47)
 

and the results are:

 

m1 =      0
d1 =      0
VSWR1 =    1.0000
Rloss1 =  313.0712 

m2 =     0.4472
d2 =    26.5651
VSWR2 =  2.6180
Rloss2 = 6.9897 

m3 =     0.5505
d3 =   -82.6171
VSWR3 =  3.4494
Rloss3 = 5.1848 

3.- Video: alternative code to draw the chart