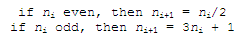Collatz
Conjecture - an approach in Matlab
The Collatz conjecture
(named after Lothar Collatz) is an
unsolved
conjecture in mathematics. This conjecture is also known
as 3n + 1,
Ulam’s,
Kakutani’s
problem, Thwaites’,
Hasse's
algorithm, or the Syracuse
problem; the sequence of numbers involved is referred to
as the hailstone
sequence.
This is the sequence:
take a positive integer n;
if n is
even, divide it by 2, and that's the next number in the sequence; if n is odd,
the next number is 3n
+ 1 (this process has been called ‘Half or Triple Plus
One’, or HPTPO). Repeat the process indefinitely... or until you reach
1.
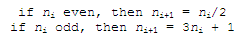
The conjecture is that no
matter what number you start with,
you will
always eventually get to 1. So far, no one has found a
case when this
doesn’t happen, but the conjecture hasn’t been formally demonstrated.
A possible code in Matlab is as follows:
function [ns,
seq] = collatz(n)
%
Your first number in the sequence is n
seq(1) =
n;
%
You position an index on the next element of the sequence
i = 2;
%
Repeat the iteration until you find a 1
while
seq(i-1) ~= 1
% Use a
modulus after division
to find an even/odd number
if mod(seq(i-1),
2) == 0
% Step
taken if even
seq(i) = seq(i-1)/2;
else
% Step
taken if odd
seq(i) = 3*seq(i-1) + 1;
end
%
Increment your index
i =
i+1;
end
%
Find the length of the sequence
ns
=
length(seq);
Now, let’s try our Collatz-sequence
function from another script
or from the command window. We start with 12 and want to know the
sequence and
the number of elements in that sequence.
clc;
clear
[n, seq]
= collatz(12)
and we
get:
n = 10
seq = 12
6
3
10
5
16
8
4
2
1
Now, let’s say that we’d like to know what natural number up
to 20 produces the longest sequence.
We can try something like
this:
clc;
clear
%
We're going to start the sequences with integers up to 20
for i = 1 :
20
% We
perform the function and
get the number of elements
% in the
sequence and the
sequence itself
[n(i), seq{i}] = collatz(i);
end
%
We find out what's the maximum number of steps found
[max_steps,
ix] = max(n)
%
We display the appropriate indexed sequence
seq{ix}
And we get:
max_steps = 21
ix = 18
ans =
18
9 28
14
7
22
11 34
17
52
26
13 40
20
10
5
16
8
4
2
1
This means that if we
start our sequence with 18, we get 21
elements in the sequence.
From 'Collatz Conjecture' to Matlab home
From 'Collatz
Conjecture' to 'Flow Control Menu'

|