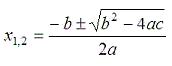Learn to solve quadratic equations
We are
going to create now a Matlab program that calculates the quadratic roots (roots
of quadratic
equations). The equation must be in the following form:
ax2
+ bx + c = 0
where a, b, and c are real
coefficients.
The
formula used to calculate the roots is:
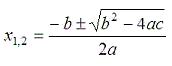
Naturally,
we have to deliver two x-values.
The
following video shows you an example of what we want to accomplish. We
use an online calculator to solve this problem. After the video, we
show you the equivalent code that we have to implement to get the same
results.
The
m-file
that we might use to accomplish this task is very simple:
function
x = rqe(a,b,c)
x(1) =
(-b + sqrt(b^2 - 4 * a * c))/(2*a);
x(2) =
(-b - sqrt(b^2 - 4 * a * c))/(2*a);
We
enter the coefficients as parameters when we call the function. We
assign
to variables x(1)
and x(2)
the calculated values using the formula, and the returning result x
is a
vector containing x(1)
and x(2).
We
could use the following Matlab code instead, to return two separate
variables:
function
[x,y] = rqe2(a,b,c)
x = (-b
+ sqrt(b^2 - 4 * a * c))/(2*a);
y = (-b
- sqrt(b^2 - 4 * a * c))/(2*a);
If we
want to compute the roots of the following expression:
2x2
+ x - 1 = 0
We can
call our function (first code) like this:
x =
rqe(2, 1, -1)
and we
get from Matlab:
x =
0.5000
-1.0000
We can
call our second function (second code above) like this:
[m, n] =
rqe2(2, 1, -1)
and
we
get from Matlab:
m
=
0.5000
n
=
-1
From
'Quadratic
Equations' to
home
From
'Quadratic Equations' to 'Matlab Cookbook'

|