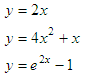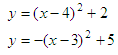Nonlinear
Simultaneous Equations
We’re
going to develop a Matlab function to solve systems of nonlinear simultaneous equations.
points, we
need to be aware of the solution found, the number of iterations
needed, the
number of function evaluations needed, and the exit flag value. This
helps us
know whether the found solution is good or bad. It’s important to note
that this minimization
or optimization
function (fminsearch) doesn’t solve simultaneous equations. We have to adapt
the system or formulate
the problem in such a way that we can accomplish this.
In this particular case, we’re going to express the nonlinear system as
a scalar
value, and it’s going to be reduced to its minimum value by fminsearch.
That
value will be the solution to our problem. Naturally, different
tolerances or starting points deliver
different results. Only one intersection is found for every starting
point,
even though the nonlinear system may have more than one
solution. If we have this nonlinear system of simultaneous equations:
We can
express the system in Matlab as a function delivering a scalar:
e1 =
abs(y1 - y2); y =
max([e1 e2 e3]);
Finally,
we can minimize this type of systems with an optimization instruction.
We pass
two parameters: the name of the nonlinear system and the starting point
(we’re
using the default options, which can be modified with ‘optimset’). fx = 'nls1'; The
answer is:
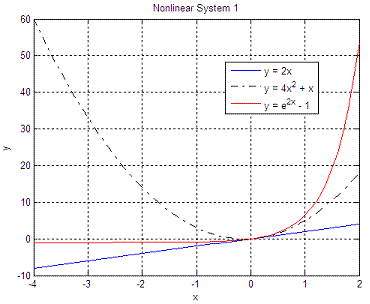
Now, we
can try a different starting point, to compare solutions: x0
= 10 The new
answer is: x_sol
=
0 Note that the solution in both cases is the same, but the number of function evaluations to get to the solution is not the same. If the curves are very
complex, with many ups and downs, the algorithm
might not get a good answer. You should try then several starting
points.
Another
example. Let’s solve this system:
function y =
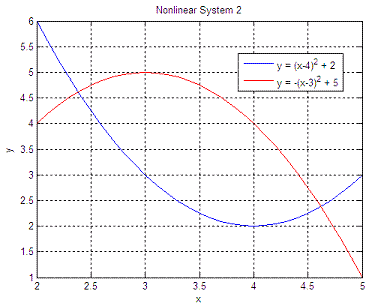
nls3(x) Each run finds only one answer. We must try
different starting points to find different intersections. We run
the script like this:
x0 = 15 The
two solutions are: x_sol
=
2.3820 x_sol =
4.6180
We find both solutions, x1 = 2.382 when we start at x0 = -20, and x2 = 4.618 when we start at x0 = 15. From 'Nonlinear Simultaneous Equations' to home From 'Nonlinear Simultaneous Equations' to Matlab Programming
|