Square root algorithm (example on while-loops)   

We’ll follow a different approach: an iterative method using while-loops.

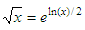The most common iterative method of square root calculation is known as the ‘Heron's method’ or ‘Babylonian method’. 

First step, estimate a number. Think of this number as your first approach to a root (the closer to the actual square root of x, the fewer iterations will be needed to achieve the desired precision). 

Second step, divide your number by this (known inexact) square root. 

Third step, take the average of the result of the second step and ‘the root’. 

Fourth step, use the result of the third step to repeat steps 2 and 3 until you have a number that is accurate enough for you.
 

The technique is a variation of the Newton-Raphson iterative solution method and it involves a simple algorithm, which results in a number closer to the actual square root each time it is repeated.
 

A code that accomplishes the algorithm is:
 

function ta = sr(x)
% Choose (arbitrarily) a first approach
fa = x/2;
% Divide your number by that first approach
sa = x/fa;
% Get the mean between the two previous numbers
ta = mean([fa sa]); 

% Repeat until you obtain a good enough root
while abs(x - ta^2) > 0.000000001
    fa = ta;
    sa = x/fa;
    ta = mean([fa sa])
end
 

We can use or try our function like this, from the command window for example:
 

format long
y1 = sr(10)
y2 = sqrt(10)

ta =    3.17857142857143
ta =    3.16231942215088
ta =    3.16227766044414
ta =    3.16227766016838

 
Our algorithm needed four iterations to obtain the final result (in y1, below). Note that only two iterations were needed to have an accuracy within three decimals. y2 is the result from the function ‘sqrt’, to compare with.
 

y1 =    3.16227766016838
y2 =    3.16227766016838
 

Another example,

y3 = sr(255)
y4 = sqrt(255)
 

ta =   34.34411196911197
ta =   20.88448273516376
ta =   16.54725251948965
ta =   15.97883290053478
ta =   15.96872262323155
ta =   15.96871942267163
 

Our algorithm needed six iterations to obtain the final result (in y3, below). Note that only four iterations were needed to have an accuracy within one decimal. y4 is the result from the function ‘sqrt’, to compare with.
 

y3 =   15.96871942267163
y4 =   15.96871942267131

 From 'Square Root algorithm' to home

 From 'Square Root algorithm to 'Flow Control'