

Binomial Distribution
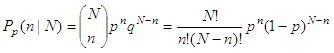 where N = the number of trials n = the exact number of successes p = the probability of success First, we can clear the current Matlab workspace and also the screen, to keep things clean... clear; clc; Then, we ask the user to enter the three required numbers... We use the 'input' function in Matlab for this purpose, n = input('Number of trials: '); x = input('Exact number of successes: '); p = input('Probability of success: '); Now, this is the main algorithm to solve the problem, m1 = log(factorial(n)); m2 = log(factorial(x)); m3 = log(factorial(n-x)); r = exp(m1 - m2 - m3 + x*log(p) + (n-x)*log(1-p)); Finally, we display the answer (the instruction 'num2str' transforms a number into a string), str = ['Probability of ' num2str(x) ' successes in ' ... num2str(n) ' trials: ' num2str(r)]; disp(str) See the example running... What is the probability of getting three heads in five tosses of a fair coin? Number of trials: 5 Exact number of successes: 3 Probability of success: .5 And the Matlab response is Probability of 3 successes in 5 trials: 0.3125 What is the probability that in five rolls of a fair die, a number 1 appears twice? Number of trials: 5 Exact number of successes: 2 Probability of success: 1/6 And the response is Probability of 2 successes in 5 trials: 0.16075 Reference: Poole, L.; Borchers, M.; Some Common Basic Programs; Osborne/McGraw-Hill; 3rd. edition; Berkeley, CA; 1979. From 'Binomial Distribution' to home From 'Binomial Distribution' to 'Probability and Statistics'
|

