Combinational logic - Basic Applications of Boolean GatesExperiments with electronic gates
The
lock on the left has four discs that can be rotated separately. When
the
notches are aligned, the metal hook is released. The only one condition
needed is
that the appropriate four notches are aligned, no matter if the left
disc is set
before the one on the right. The lock will open if you have the
correct
combination. On the
contrary, the lock on the right has only one knob, and the combination
could be
3cw – 52ccw – 20cw. This means that one must first get to number 3
going
clockwise, then to 52 counterclockwise, and finally get to number 20
clockwise.
If you use the same numbers in different order, the lock won’t open.
This is a sequential
lock, a correct sequence is important. Due to
its stability, reliability, low maintenance and ease at reading digital
displays, these days everything is going the digital way. Logic
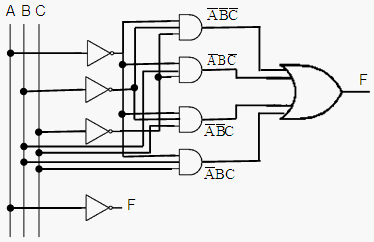
circuits can be simulated with the so called boolean or logic gates. Let’s
say that we’d like to find out the behavior of the following
combinational
circuit:
function f =
combination(x) %
We have 4 logic-AND gates %
We have 1 logic-OR gate
%
These are all the possible combinations for 3 inputs %
We give all the combinations, one at a time %
We display the results The
results are: comb_log
= 1
1
1
1
0
0
0
0 This
means that we have not only a MATrix LABoratory, but we've
got also a
circuit
logic simulator! From 'Combinational Logic' to 'Boolean Algebra'
|