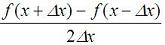[?] Subscribe To This Site

Numerical Derivative

We are going to develop a Matlab function to calculate the numerical derivative of any unidimensional scalar function fun(x) at a point x0. The function is going to have the following functionality:

Usage:    D = Deriv(fun, x0)
          fun: name of the unidimensional scalar function
  (string)
          x0: point of interest (scalar)
          D: derivative of fun at x0 (scalar)

As you may remember, the very well known way to analytically derivate any function is: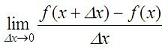

This roughly means that we have to find the value of the function in two very close values (one of them is the point of interest), get the difference of those values and divide it by the displacement of the independent variable. In other words,

First step:
Find functions for derivatives

, where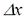

is a very small value compared to x.

Second step:
Obtain the difference function difference for derivatives .

Third step:
Divide the result above by delta x .

The result is the numerical derivative of your function.

We can implement this algorithm very easily in Matlab, in this way:

function D = Deriv(fun, x0)
% |delta| is relative to |x0|
delta = x0 / 1000;
if x0 == 0
% avoids delta = 0 (**arbitrary value**)
delta = 1e-12;
end
f1 = feval ( fun, x0 + delta );
f2 = feval ( fun, x0 - delta );
D = (f1 - f2) / (2 * delta);

Note, that we are really evaluating

algorithm for derivative

which should be the same as explained above, since the displacement is almost zero. You can try both options.

Function 'feval' evaluates a given function (the string in the parameter fun) in a specific value (number in second parameter of 'feval').

Now, let's try our derivative function. We create a function in a separate m-file:

function y = inverse(x)
y = 1/x;

And we can call it like this:

Deriv('inverse', 1)

The result is:
Expected: -1 Obtained: -1.0000

Deriv('inverse', 5)

The result is:
Expected: -0.04 Obtained: -0.0400

We can save another totally arbitrary (unidimensional scalar) function in a different m-file:

function y = myfun(x)
y = 3*x^2 + 2*x;

And we can perform the derivative in several ways...

f = 'myfun'
x = 0
Deriv(f, x)

The result is:
Expected:     2    Obtained:     2

x = 5
Deriv(f, x)
The result is:
Expected:     32    Obtained:    32.0000

Deriv(f, -3)
The result is:
Expected:    -16    Obtained:     -16.0000

Top
<Gradient>

From 'Derivative' to home
From 'Derivative' to 'Matlab Cookbook'

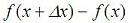footer for derivative page