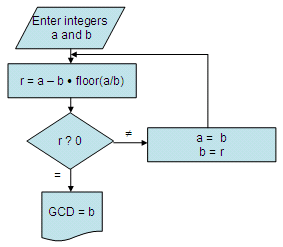
Euclidean Algorithm

This program calculates the Greatest Common Denominator (GCD) of two integers. It is based on the Euclidean algorithm for finding the GCD.

Basic Algorithm - Flow chart

This is the full Matlab program that follows the flow-chart above, without using the built-in 'gcd' instruction.

% Clears screen and deletes all the variables in the workspace
clear; clc

% Asks the user for input and takes only positive numbers into account
a = input('First number: ');
b = input('Second number: ');
a = abs(a);
b = abs(b); 

 % This is the real trick, normally performed a number of times
r = a - b*floor(a/b); 

% Repeats the operation until updates of a equal updates of b
while r ~= 0
    a = b;
    b = r;
    r = a - b*floor(a/b);
end 

% Displays the result
GCD = b

Example 1:

Run the algorithm above and enter data: 

First number: 18
Second number: 50

GCD =
     2

The built-in Matlab command 'gcd' also works on vectors. For example:

a = [50 150 20]
b = [18 115 5] 

>> gcd(a,b) 

ans =
     2     5     5