Mathematical Optimization using ScilabIn Scilab, we can perform
mathematical optimizations using
the built-in function named ‘optim’. We need to define the function to
be
optimized, with some special pecularities to take into account. Our
function not
only takes its regular arguments, but there’s also a parameter
indicating what it
is expected to deliver. The function must output its value and maybe
its
gradient and an index to notify special cases. So optim is another
non-linear optimization routine and it’s
based on derivatives. We have seen polynomial fitting
and least squares-based
algorithms in other examples. In general, the form of the function to be minimized or optimized is: [fx, gr, ind2] = f(x, ind1,
p1, p2, ...) where We are going to see a
simple example where we want to
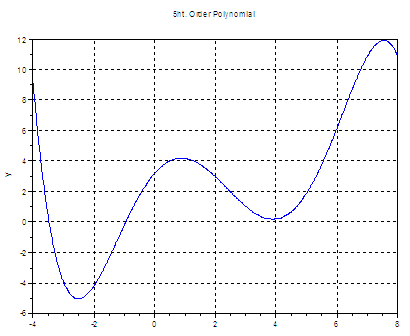
minimize a 5th. order polynomial. This is our polynomial: y = -0.0071x5 + 0.087x4 - 0.1x3 - 1.3x2 + 2.3x + 3.2
x = -4 : .01 : 8;
This is the code that we
could use to find its minimum
value: // We define the function // We define the objective
or cost function. We need to // We have to make an initial guess // Now we use the optim
function which calls the The result of our
mathematical optimization according to
Scilab is: xopt = -2.5130895 Notice that this result
is a local minimum. Actually, the
function minimum is a number that tends
toward minus infinity (not plotted). If
we start with another seed, we can get a
different result, for example x0 = 8; produces: We also can include lower
and upper bounds on x, as in x0 = 1; which now produces
another local minimum A note about the gradient
that we need to include as output: we used ‘numdiff’, which
is a numerical gradient estimation, and we can also
use http://help.scilab.org/docs/5.3.3/en_US/optim.html Maybe you're interested in: Non-gradient-based optimization in Matlab Steps of a strategic optimization From 'Mathematical Optimization' to home From 'Mathematical Optimization' to Scilab
|