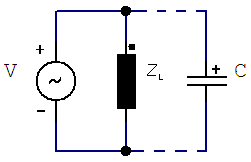
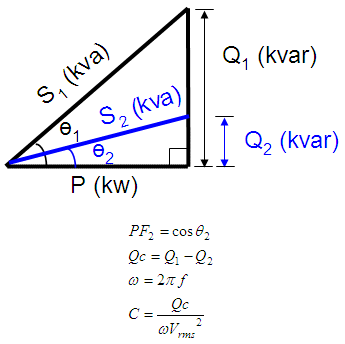Power Factor Correction Capacitors

 
This is a graphical concept of what we’re trying to do for this correction:

 
where
Vrms = 220 VAC
f = 60 Hz
PF = 0.82
P = 5.4 kW
 

Our task is to find the capacitor C to get a corrected PF = 0.92. 

We know that AC power flow has three components: real or active power P, measured in watts (W); apparent power S, measured in volt-amperes (VA); and reactive power Q, measured in reactive volt-amperes (var). The following right-triangle describes the relationship for those three components.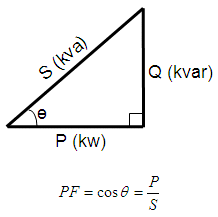

 

If we add a capacitor in parallel, the reactive power of the system will change (decrease). The difference between the original reactive power Q₁ and the resulting reactive power Q₂ (after placing the capacitor) is called Qc. The final capacitor is a value depending on the reactive power Qc (in var), the frequency (in Hz) and the voltage at the load (Vrms). This diagram shows the idea and we present the formulas.

We can develop a very simple code to find out how to correct the power factor in the system above. We only need a little bit of knowledge of basic trigonometry... 

clear all, clc 

% Known data: voltage source, frequency, starting power factor
% and corrected (final) power factor
Vrms = 220
f = 60
P = 5.4e3
fp1 = 0.82
fp2 = 0.96 

% We calculate the initial angle, apparent and reactive powers
th1 = acosd(fp1)
S1 = P/fp1
Q1 = S1 * sind(th1) 

% We calculate the final angle, apparent and reactive powers
th2 = acosd(fp2)
S2 = P/fp2
Q2 = S2 * sind(th2) 

% We calculate the difference in reactive powers
Qc = Q1 - Q2 

% We express the capacitor in microfarads
C = [num2str(Qc / (2*pi*f * Vrms^2)*1e6, 4) ' uF'] 

The results shown in the command window are: 

Vrms = 220
f = 60
P = 5400
fp1 =  0.8200
fp2 =  0.9600
th1 =  34.9152
S1 =  6.5854e+003
Q1 =  3.7692e+003
th2 =  16.2602
S2 =  5625
Q2 =  1.5750e+003
Qc =  2.1942e+003
C = 120.3 uF