RC Circuit 

Transient Analysis with Matlab

Considering the RC Circuit (also called RC network) shown in this figure 

we can use the Kirchhoff’s current law (KCL) to write the following equation

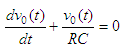The solution to the equation above is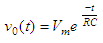

 

where
V_m is the initial voltage across the capacitor
RC is the time constant 

This solution represents the voltage across a discharging capacitor. 

Now, to obtain the voltage across a charging capacitor, let us consider this figure that includes a voltage source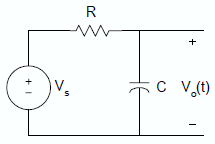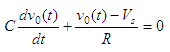 

Again, using KCL, the equation describing the charging RC circuit is

If the capacitor is not charged initially, that is v₀(t) = 0 when t = 0, then the solution to the equation above is given by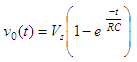 

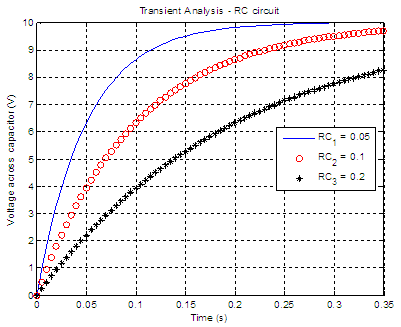
The following examples illustrate the use of Matlab for solving problems
related to RC circuits.

Example 1 – Charging circuit

Assume that for the charging RC circuit above Vs = 10 volts and C = 10 microfarads. Plot the voltage across the capacitor if R equals 5k ohm, 10k ohms and 20k ohms. This just means that we are going to explore three time constants. 
 

This code is one simple solution to the problem  

% Define the voltage source
Vs = 10;
% Define the capacitor in the circuit
C = 10e-6;
% Define the time lapse that we're going to explore
t = 0 : 0.005 : 0.35;
 

% Define the resistors in each time constant and
% calculate the voltage across the capacitor
R1 = 5e3;
tau1 = R1*C;
V1 = Vs * ( 1 - exp(-t/tau1) );
 

R2 = 10e3;
tau2 = R2*C;
V2 = Vs * ( 1 - exp(-t/tau2) );
 

R3 = 20e3;
tau3 = R3*C;
V3 = Vs * ( 1 - exp(-t/tau3) );
 

% Plot the responses, all at once
plot(t, V1, 'b-', t, V2, 'ro', t, V3, 'k*')
grid on
title('Transient Analysis - RC circuit')
xlabel('Time (s)')
ylabel('Voltage across capacitor (V)')
legend(['RC_1 = ' num2str(tau1)],...
       ['RC_2 = ' num2str(tau2)],...
       ['RC_3 = ' num2str(tau3)], 'location', 'best')
 

The resulting plot is
 

 
From the resulting plot of our transient analysis, we see that if the time constant is small, it takes a shorter time for the capacitor to charge up (the smaller the time constant the faster the circuit response). We also can see that when the time constant is reached by each response, we have obtained more or less the 63% of the total voltage to be taken (that’s why the RC value is called the time constant).  

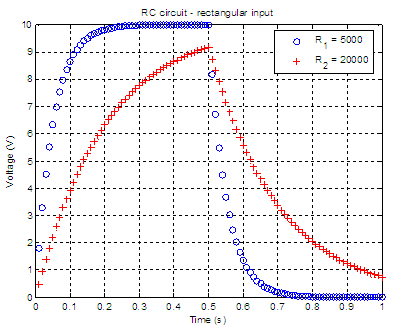
Example 2 -  Charging / discharging RC circuit

In the same charging circuit above, the input voltage is now a rectangular pulse with an amplitude of 10 volts and a width of 0.5 seconds. If C = 10 microfarads, we’ll plot the output voltage, v₀(t), for a resistance R equal to 5k ohms, and 20k ohms. The plots should start from 0s and end at 1s. 
 

We are going to develop a function that will return the voltage and corresponding time of the response. We need to use the two formulas mentioned previously and that’s why we separate our code in two halves.

The input parameters are the voltage source (vs), the resistor (r) and capacitor (c). 

function [v, t] = rectangular_RC(vs, r, c)
tau = r * c; 

% First half of the pulse: 0.01 to 0.5 seconds
% Use the correct formula.
t1 = linspace(.01, 0.5, 50);
v1 = vs * (1 - exp(-t1/tau)); 

% Second half of the pulse: 0.51 to 1 seconds.
% Take into account the max voltage reached.
% Use the appropriate formula.
Vm = v1(end);
t2 = linspace(0.51, 1, 50);
v2 = Vm * exp(-t1/tau); 

Now, we are going to call the function from our main code, like this 

% Given constants
vs = 10;
c = 10e-6; 

% Case 1. R = 5k ohms
r1 = 5e3;
[v1, t1] = rectangular_RC(vs, r1, c); 

% Case 2. R = 20k ohms
r2 = 20e3;
[v2, t2] = rectangular_RC(vs, r2, c); 

% Plot the responses
plot(t1, v1, 'bo', t2, v2, 'r+')
grid on 

% Add labels
title('RC circuit - rectangular input')
xlabel('Time (s)')
ylabel('Voltage (V)')
legend(['R_1 = ' num2str(r1)], ...
       ['R_2 = ' num2str(r2)])
 

 The resulting plot is

We can see that the first circuit reaches the maximum voltage of the source. The second circuit started its discharge before reaching the maximum voltage.