

Polygon Area
The formula used to calculate the area is: area = [(x1+x2)(y1-y2)+(x2+x3)(y2-y3)+ ... +(xn+x1)(yn-y1)]/2 where n is the number of vertices. Let's assume that we have our vertices in two different vectors, for examplex = [0 1 4 5 7 9 12 14 13 15 15 13 5 4 0]; y = [4 7 8 10 11 10 9 8 4 4 1 0 1 2 4]; Note that the first and last vertices are the same, to close the polygon area. We can plot this polygon in Matlab very easily. If we use the instruction 'plot(x, y, '-o')', we obtain the following figure (just to visualize what we are doing): 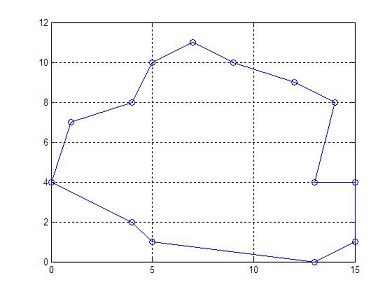 If we use the instruction 'area(x,y)', we obtain the following figure (to learn another way to plot vectors): 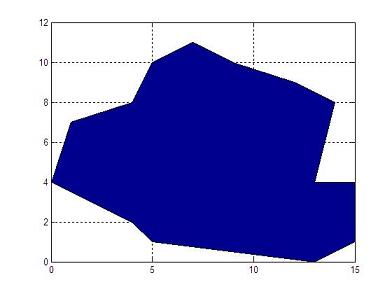 Now, we prepare a function with the vertices in input vectors x and y. The output scalar variable is p_area. function p_area = area_calc(x,y) % Get the number of vertices n = length(x); % Initialize the area p_area = 0; % Apply the formula for i = 1 : n-1 p_area = p_area + (x(i) + x(i+1)) * (y(i) - y(i+1)); end p_area = abs(p_area)/2; We can call the function with a simple line, like this: a1 = area_calc(x,y) And we obtain from Matlab: a1 = 108 It's important to mention that we can save all the code above, since Matlab includes the built-in function 'polyarea', that we can call in this manner: a2 = polyarea(x,y) which produces the same result. a2 = 108 Another example? Let's execute this code... x = [0 0 3 3]; y = [0 1 1 0]; a1 = area_calc(x,y) a2 = polyarea(x,y) And the result is... a1 = 3 a2 = 3 ... as expected. From 'Polygon Area' to home From 'Polygon Area' to 'Matlab Cookbook'
|

