

Polynomial Roots - 'Zero finding' in MatlabTo find polynomial roots
(aka 'zero finding'
process), Matlab has a specific command, namely 'roots'.
A polynomial is an expression of finite length built from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents. If you type on the command window: >> help roots the Matlab online help will display: ROOTS Find polynomial roots. ROOTS(C) computes the roots of the polynomial whose coefficients are the elements of the vector C. If C has N+1 components, the polynomial is C(1)*X^N + ... + C(N)*X + C(N+1). This means that the coefficients of the polynomial are placed in a vector C and the built-in function returns the corresponding roots or zeros. It is simple to use, but care is needed when entering the coefficients of the polynomial. For example, find the roots of the equation f(x) =
3x5 − 2x4 + x3
+ 2x2
− 1
You can use the simple Matlab code: c = [3 -2 1 2 0 -1]; roots(c) And Matlab will deliver the following five zeros (x-values that produce a function f(x) = 0): ans = 0.5911 + 0.9284i 0.5911 - 0.9284i 0.6234 -0.5694 + 0.3423i -0.5694 - 0.3423i There’s a couple of things to note from this example: The polynomial’s coefficients are listed starting with the one corresponding to the largest power. It is important that zero-coefficients are included in the sequence where necessary. A polynomial of order p has p + 1 coefficients, this is, a quadratic has three coefficients and a polynomial of degree p will have p roots. As long as the coefficients of the polynomial are real, the roots will be real or occur in complex conjugate pairs. Built-in Command fzeroThe Matlab command 'fzero' is powerful. It actually chooses which internal method should be used to solve a given problem, and can be used for non-polynomical functions.Let us try the form of the command options = optimset('disp','iter'); fzero('func', 3, options) The command uses many different forms but here we are looking for a root of the function defined in 'func.m' near the value x = 3 and the options are set to 'display iterations'. For example, determine the zero of the function f(x) = 3x − 2x2 sin(x), closest to x = 2. A fast plot of the function (for exploration purposes) results in: 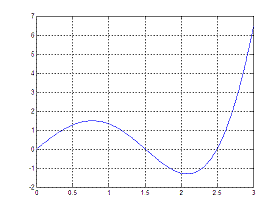 So we need to set up the code: function mf = myfunction(x) mf = 3*x – 2*x.ˆ2.*sin(x); and later we may use the inline command fzero like this (no input vector is needed) >> fzero('myfunction', 2) The Matlab answer is: ans = 1.5034 More operations with polynomials From 'Polynomial Roots' to home From 'Polynomial Roots' to 'Matlab Cookbook II'
|

